呦呼～ 大家早安！
今天要來介紹的主是N-gram，也是一種可以用來統計詞頻的方式，也可以算是最初代語言模型的一種！
我們昨天有提到Bag Of Words 他的缺點就是他不會考量到語序，所以以「我喜歡你」跟「你喜歡我」這兩句話對電腦來說是一樣的，而今天要介紹的N-gram 的方式就是有考慮到順序這點，事不宜遲，我們趕快開始吧！

N-Gram 是什麼？

N-Gram的N其實就是代表我們「一次看幾個詞」。如果 N=1，表示一次只看一個詞，以一個詞作單位，我們也稱 Unigram。如果 N=2，就叫 Bigram，表示一次看兩個連續的詞，如果 N=3，就叫 Trigram，表示一次看三個連續的詞，以此類推。N可以是任何數字，N 設多少，就會用 N 個連續的詞來做切分和統計。
可能說到這邊有點抽象，我們舉「我喜歡狗狗」當作例子來說明：

unigram -> [我/喜/歡/狗/狗]
bigram -> [我喜/喜歡/歡狗/狗狗]
trigram -> [我喜歡/喜歡狗/歡狗狗]

在這邊你可能就會發現，unigram 跟 Bag of Words 差不多，因為它只是在數詞在文本的出現次數；但 Bigram、Trigram 就能捕捉到「連續詞的搭配關係」，這樣「我喜歡你」和「你喜歡我」就不會再被當成完全相同的東西了。

而N-Gram 最大的好處，就是能在簡單的詞頻統計中帶入「一點點上下文資訊」，所以它也常被用來計算一個句子出現的機率，也是最早的語言模型的始祖之一，可以用來預測下一個詞的可能性。舉例來說，當我們看到「颱風天就是要＿＿」這個句子時，模型很可能會判斷下一個詞是「泛舟」而不是「吃飯」，因為在語料中「颱風天就是要泛舟」的出現頻率遠高於「颱風天就是要吃飯」。它的計算方式其實也很直觀，就是比較「颱風天就是要」後面接「泛舟」的機率，和接「吃飯」的機率，誰比較高就預測誰。

而他是怎麼算的呢？N-Gram 的核心假設就是 馬可夫假設 (Markov Assumption)：
簡單來說，就是當前詞的出現機率只會依賴前面有限的幾個詞（而不是整個句子）
什麼意思呢？假設我們要計算一句話出現的機率，應該要考慮所有條件機率：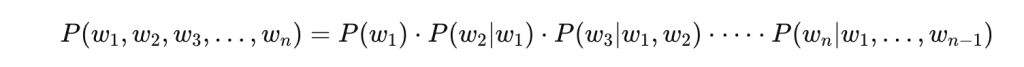

但這樣等於要同時考慮前面所有詞，實務上幾乎不可能計算。而馬卡夫假設就是當前詞只受到他前面的N-1個詞影響而已！
也就是說以 Bigram (N=2)模型的計算方式可以大大簡化成：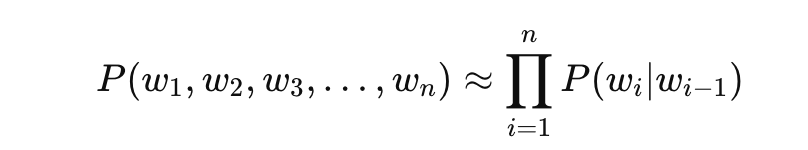

N-Gram 缺點

當然，N-Gram 雖然直觀好理解，但他也有一些淺在的缺點：

1. 無法捕捉長距離的語意：由於馬可夫假設，N-Gram 只會考慮前面 N-1 個詞所以他無法捕捉更長的語意關係。
2. 數據稀疏問題：N-Gram 需要靠「統計共現頻率」來計算機率，也就是算N個詞一起出現的機率，但現實中也許大部分的詞組合在語料中根本沒出現過，導致機率無法估算。舉例來說許多新詞一開始不會出現在語料庫中，這樣計算出來出現的機率就會是0，所以一般我們會再用smoothing 的方式解決這個問題。

好啦～那我們來小小總結一下今天的重點！
今天我們介紹了 N-Gram 這個概念。跟昨天的 BOW 不同，BOW 只關注詞有沒有出現、出現幾次，而 N-Gram 則是去觀察「哪些詞會連在一起」，並計算它們的機率。透過這種方式，模型能保留一點語序資訊，用來計算句子的機率，甚至預測下一個詞。
當然，N-Gram 也還是有一些限制，因此才會有後來更進階的方法出現，用來改善這些問題～我們之後也會慢慢聊到！

今天就先這樣～ 我們明天見！